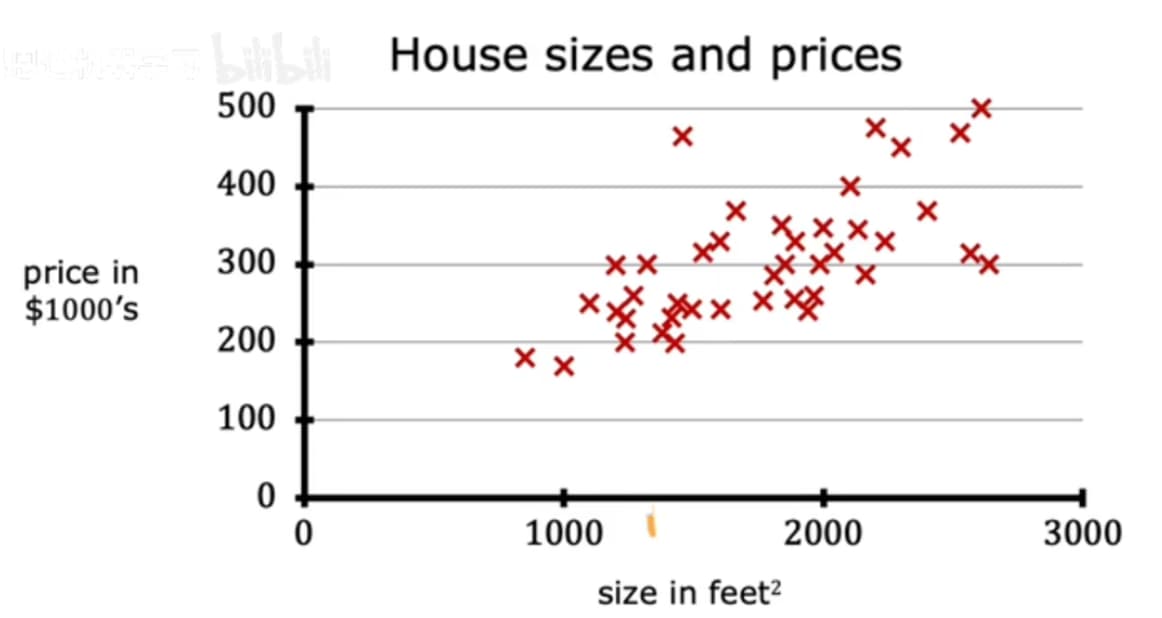
//辅助房地产估价 (拟合直线
核心概念:
- 用于训练模型的数据集称为训练集
- 输入变量(x) :也称为特征或输入特征//input
- 输出变量(y) :输出的量//output target
(x,y)即一个训练示例, $x^{(i)}$ , $y^{(i)}$ 表示第i个训练示例
训练模型:将训练集提供给学习算法,
算法会产生功能function $x \to f \to \hat y$
该过程即:feature -> model -> prediction
$f_{(w,b)}(x)=wx+b$
成本函数(也称为代价函数)
成本函数的思想是机器学习中最普遍和最重要的思想之一,用于线性回归和训练世界上许多最先进的人工智能模型。
👉如何构建成本函数:
平方误差成本函数
\(J_{(w,b)}= \frac{1}{2m} \sum\limits_{i=1}^m(\hat{y}^{(i)} -y^{(i)})\)
\(J_{(w,b)}= \frac{1}{2m} \sum\limits_{i=1}^m(f_{(w,b)}(x) -y^{(i)})\)
P.S.
- m指的是训练示例个数;
- 将每个预测的y值与真实的y值相差平方求和;
- 额外除的2是为了后续的计算更加简洁;
目标是求: $minimize_{w,b} J(w,b)$
让成本函数尽可能的小,模型的准确度也就越高
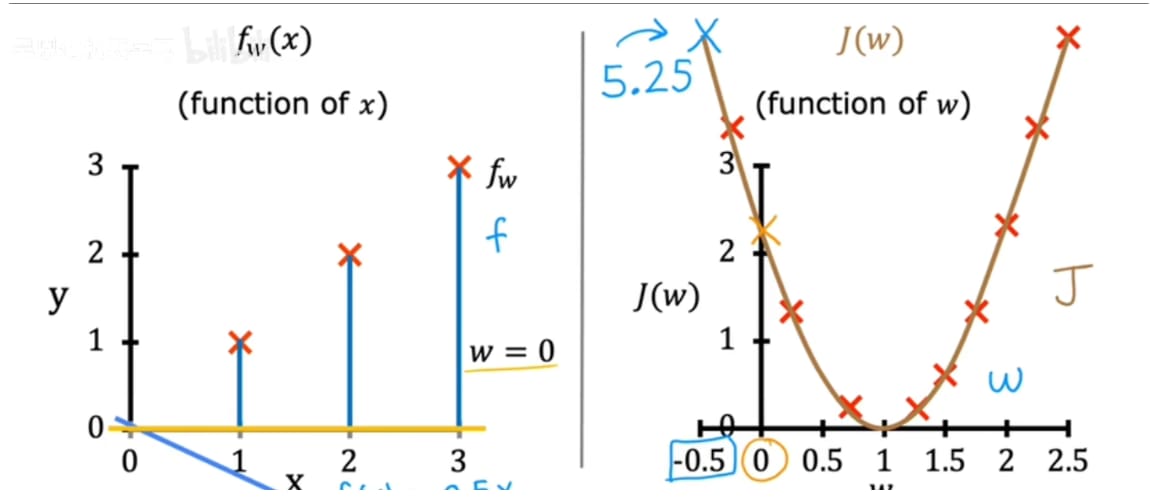
👉成本函数的可视化
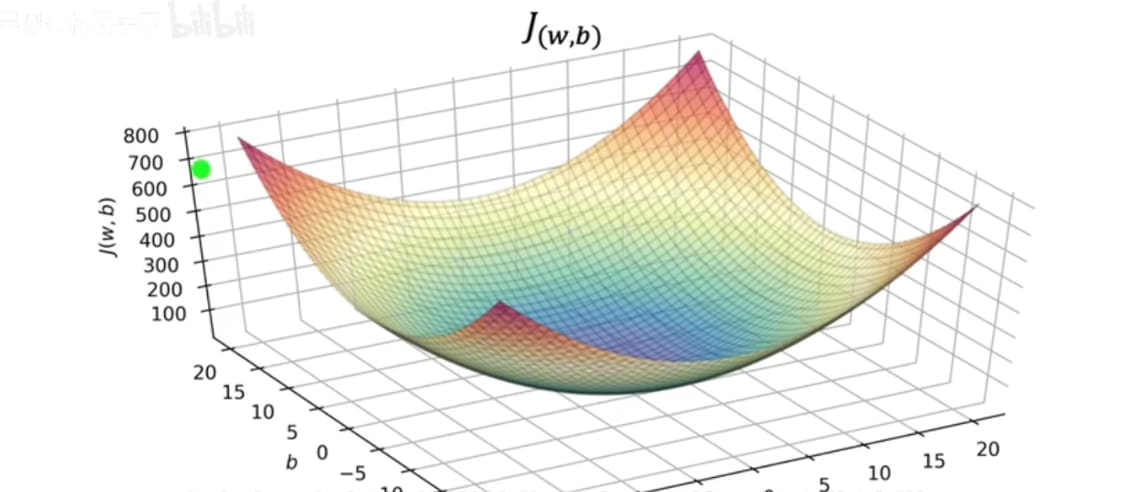
若规定了b一定 则图像为二维坐标图像 (汤碗侧切图状)
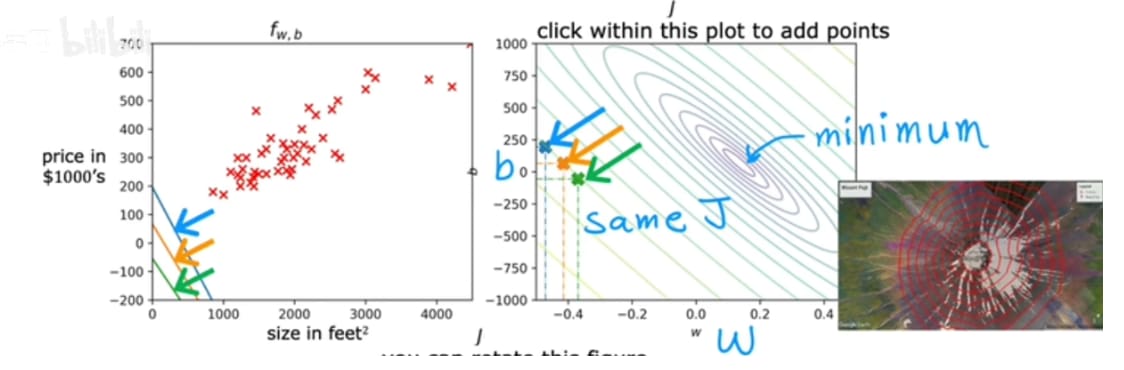
然而用3D图形表示非常不便,于是可以化成等高线地形图的模式去表示
梯度下降算法
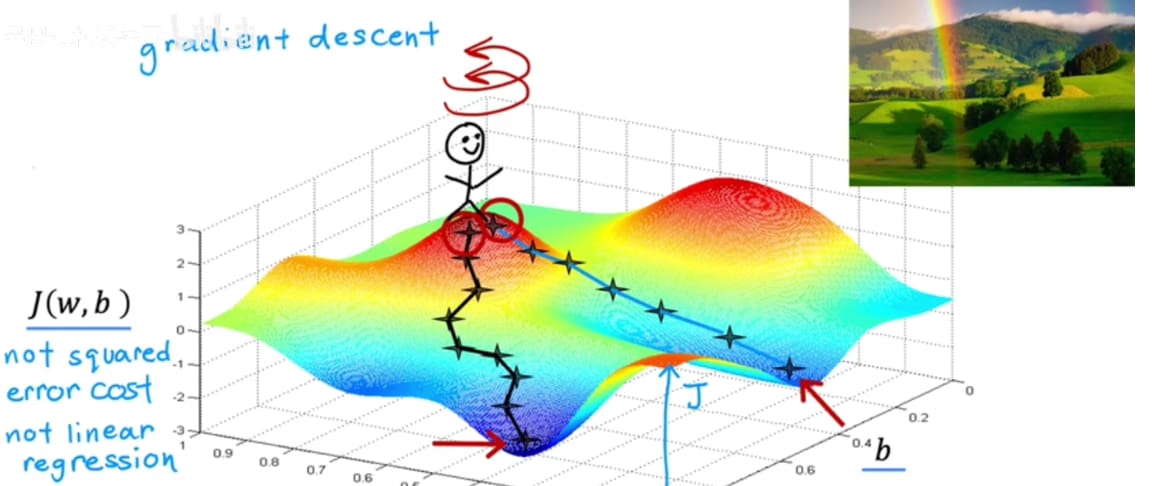
在成本函数图像上,从最高点开始 不断“环顾四周”找到斜率最大的方向并移动一段极小的距离,继续找下降斜率最大的方向,如此重复。
\(w=w-\alpha \frac{d}{dw} J_{(w,b)}\)
\(b=b-\alpha \frac{d}{db} J_{(w,b)}\)
//‘=’作为赋值运算符;$\alpha$ 被称为学习率;学习率通常是0到1之间的一个小正数
$\alpha$ 所做的是控制下坡的距离(每一步的步长) 在曲面图图形中,我们需要采取一些小步子,直到到达值的底部;
在梯度下降算法中,我们需要不断重复上述两个公式,直到算法收敛(达到局部最小值)
学习率
👉如果学习率的值过于大会怎么样?
有可能因为步长过长导致越过了成本函数的最小值
梯度下降算法实现
# 导入库
import torch
import numpy as np
from pyecharts.charts import Line
from pyecharts.options import TitleOpts, ToolboxOpts
# 数据集导入
x = np.array([0.18, 0.1, 0.16, 0.08, 0.09, 0.11, 0.17, 0.15, 0.14, 0.13])
y = np.array([0.18, 0.1, 0.16, 0.08, 0.09, 0.11, 0.17, 0.15, 0.14, 0.13])
# 确定学习率
lr = 0.01
# 初始化 w,为了减小难度暂时不考虑 b 的赋值
w = 10
# epoches 为循环进行的次数
epoches = 500
# 先设置梯度为 0
grad = 0
# 计算损失函数
def loss_new(x, y, w):
return 0.5 * np.sum((w * x - y) ** 2)
# 计算梯度
def grad_new(x, y, w):
return np.mean((x * w - y) * x)
# 核心部分 -- 迭代
list_w = []
list_loss = []
list_grad = []
list_i = []
for i in range(epoches):
grad = grad_new(x, y, w)
# 更新参数
w = w - lr * grad
loss = loss_new(x, y, w)
print(f"第{i + 1}次迭代,梯度为{grad}, 权值为{w}, 损失值为{loss}")
list_w.append(w)
list_i.append(i)
list_loss.append(loss)
list_grad.append(grad)
# 绘制梯度与迭代次数的关系图
line1 = Line()
line1.add_xaxis(list_i)
line1.add_yaxis("梯度", list_grad)
line1.set_global_opts(
title_opts=TitleOpts(title="梯度与迭代次数的关系", pos_left="center", pos_bottom="1%"),
toolbox_opts=ToolboxOpts(is_show=True),
)
line1.render()
# 绘制损失值与参数的关系图
line2 = Line()
line2.add_xaxis(list_w)
line2.add_yaxis("损失值", list_loss)
line2.set_global_opts(
title_opts=TitleOpts(title="损失值与参数的关系", pos_left="center", pos_bottom="1%"),
toolbox_opts=ToolboxOpts(is_show=True),
)
line2.render()
### 运行结果大致情况
